15 Contoh Soal Plus Jawaban dan Pembahasan TKA SMA 2025 Matematika Wajib

Matematika menjadi salah satu mata pelajaran yang menakutkan Untuk beberapa siswa. Tetapi, tidak bisa dihindari matematika menjadi salah satu mata pelajaran wajib yang harus dilalui siswa Ke Tes Kemampuan Akademik (TKA).

Kementerian Pembelajaran Dasar dan Menengah (Kemendikdasmen) Ke dasarnya sudah menyebutkan kisi-kisi materi apa saja yang diujikan Untuk mapel matematika wajib. Materi yang termasuk adalah bilangan, aljabar, geometri dan pengukuran, data dan Potensi, serta trigonometri.

Dikutip Bersama Bacaan TKA Mapel Wajib SMA/MA 2025/2026 karya The King Forum Tentor Indonesia berikut ini 15 contoh soal plus jawaban dan pembahasan TKA SMA 2025 mata pelajaran matematika wajib. Yuk asah kemampuanmu Ke sini!

15 Contoh Soal TKA Mapel Matematika Wajib

1. Jika x adalah jumlah bilangan prima Antara 30 dan 50 dan y adalah jumlah bilangan genap Antara 30 dan 50, maka….

A. x > y
B. x < y
C. x = y
D. hubungan x dan y tidak dapat ditentukan
E. x = y

Jawaban: B. x < y
Pembahasan:

Bilangan yang merupakan kelompok Bersama x dan y terdapat Ke rentang yang sama Antara 30 dan 50. Bersama Meramalkan saja, banyaknya bilangan prima yang ada lebih sedikit daripada banyaknya bilangan genap.
Maka, secara logika x < y.

Tetapi, bila dihitung maka:
x = 31 + 37 + 41 + 43 + 47 = 199
y = 32 + 34 + 36 + 38 + 40 + 42 + 44 + 46 + 48 = 360

Supaya, x < y

2. Perbaikan sebuah gedung direncanakan selesai Di 45 hari Bersama pekerja sebanyak 15 orang. Sesudah 5 hari pelaksanaan dihentikan Di 10 hari Sebab keterlambatan kedatangan bahan perbaikan. Jika perbaikan harus selesai tepat waktu sesuai Wacana, maka tambahan pekerja yang diperlukan adalah … orang.

A. 5
B. 10
C. 15
D. 20
E. 25

Jawaban: A. 5
Pembahasan:

Tambahan pekerja = banyak pekerja awal x lama libur/sisa hari (sesuai target)

Tambahan pekerja =
15 x 10
= ——-
45-5-10

15 x 10
= ——
30

= 5 orang

3. Jika 2^y+3x = 32 dan xlog(x+2)-3xlog2= -1, maka 2x + y = ….

Jawaban: 3
Pembahasan:

Sifat logaritma: log a – log b = log (a/b)

2^y+3x = 2^5 -> 3x + y = 5

Maka:
xlog(x+2)-3xlog2 = -1
xlog (x+2/8) = -1
xlog (x+2/8) = xlog(1/x)
x+2/8 = 1/x
x^2 + 2x – 8 = 0
(x+4)(x-2) = 0

x + 4 = 0 atau x – 2 = 0
x = -4 (TM) atau x = 2

Sebagai x = 2, maka”

3×2 + y = 5
y = 5 – 6
y = -1

Supaya:

2x + y = 2 x 2 -1 = 3

4. Akar-akar persamaan kuadrat x^2 + (p+1)x + 8 = 0 adalah α dan β.

Jika α = 1/2β dan α, β positif, maka nilai p adalah ….

A. 8
B. 7
C. 6
D. -7
E. -6

Jawaban: D. -7
Pembahasan:

Rumus jumlah dan hasil kali akar persamaan kuadrat ax^2 + bx + c = 0 adalah:

x1 + x2 = -b/a
x1 . x2 = c/a

Bersama persamaan x^2 + (p+1)x + 8 = 0, diperoleh:

α + β = -b/a = -p-1 dan αβ = c/a = 8

Sebab nila α = 1/2β, maka:

α x β = 8
α x 2α = 8
2α^2 = 8
α^2 = 4
α = 2

α + β = -p – 1
α + 2α = -p – 1
3α = -p – 1
3×2 = -p – 1
6 = -p – 1
p = -7

5. Diketahui fungsi f:R -> R dan Forumekonomiglobal:R -> R Bersama Forumekonomiglobal(x)= -x + 3. (fog)(x) = 4x^2 – 26x + 32, maka nilai f(1) adalah ….

A. -5
B. -4
C. -3
D. 3
E. 4

Jawaban: B. -4
Pembahasan:

(gof)(x) artinya substitusikan fungsi f(x) Ke Forumekonomiglobal(x)
f^-1(x) o f(x) = I(x)

Misalkan h(x) = 4x^2 – 26x + 32, maka:
(fog)(x) = 4x^2 – 26x + 32
f(x) o Forumekonomiglobal(x) = h(x)
f(x) o Forumekonomiglobal(x) o Forumekonomiglobal^-1(x) = h(x) o Forumekonomiglobal^-1(x)
f(x) = h(Forumekonomiglobal-1(x))

Kita tentukan dahulu Forumekonomiglobal^-1(x).
Forumekonomiglobal(x) = -x + 3
y = -x + 3
x = -y + 3
maka Forumekonomiglobal^-1(y) = -y + 3
Supaya didapat Forumekonomiglobal^-1(x) = -x + 3

f(x) = h(Forumekonomiglobal^-1(x))
f(x) = 4(-x + 3)^2 – 26(-x+3)+32
f(1) = 4(-1+3)^2 – 26(-1 + 3)+ 32 = -4

Karena Itu, nilai f(1) adalah -4.

6. Keliling sebuah persegi panjang adalah 28 cm, sedangkan panjangnya 2 cm lebih panjang Bersama lebarnya. Luas persegi panjang tersebut adalah ….

A. 48 cm^2
B. 44 cm^2
C. 28 cm^2
D. 14 cm^2
E. 8 cm^2

Jawaban: A. 48 cm^2
Pembahasan:

Rumus keliling persegi panjang = 2p+2l

Misal:
K = keliling persegi panjang
p = panjang persegi panjang
l = lebar persegi panjang

Diketahui: K = 28 cm dan p = 2 cm + l

Supaya:

K = 2(p+l)
28 = 2(2+ l + l)
28/2 = 2 + 2l
14 = 2 + 2l
14-2 = 2l
12 = 2l
l = 12/2 = 6

Maka: p = 2+6 = 8 cm

Karena Itu, luas persegi panjang tersebut adalah:

L = p x l = 8 x 6 = 48 cm^2

7. Ke tahun 2016, umur seorang ibu tiga kali umur anaknya. Ke tahun 2010 umur ibu lima kali umumr anaknya. Jumlah umur mereka Ke tahun 2020 adalah ….

A. 52 tahun
B. 54 tahun
C. 56 tahun
D. 62 tahun
E. 64 tahun

Jawaban: C. 56 tahun
Pembahasan:

Misalkan:
umur ibu tahun 2016 = x
umur anak tahun 2016 = y

– Ke tahun 2016, umur seorang ibu tiga kali umur anaknya, maka x = 3y … (i)
– Ke tahun 2010 umur ibu lima kali umur anaknya, maka: x – 6 =5(y-6) …. (ii)

Substitusi persamaan (i) Ke persamaan (ii), Akansegera diperoleh:

x – 6 = 5(y – 6)
3y – 6 = 5y – 30
2y = 24
y = 12

Supaya:

x = 3y
x = 3 x 12
x = 36

Jumlah umur ibu dan anak Ke tahun 2020 adalah:

(x + 4) + (y + 4) = (36 + 4) + (12 + 4) = 56 tahun.

8. Diketahui sebuah matriks sebagai berikut:

dan A x B = C. Maka, nilai Bersama a + b = ….

A. -6
B. -5
C. -1
D. 1
E. 5

Jawaban: C. -1
Pembahasan:

Rumus perkalian matriks:

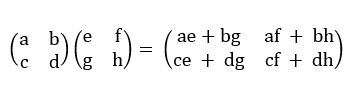Soal matriks matematika Foto: The King Forum Tentor Indonesia

A. B = C

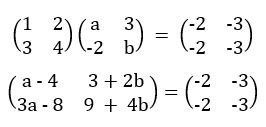Soal matriks matematika Foto: The King Forum Tentor Indonesia

Maka didapat:

a – 4 = -2 <–> a = 2
3 + 2b = -3 <–> b = -3
Supaya, a + b = 2 + (-3) = -1

9. Diketahui Un Berkata suku Ke-n suatu barisan geometri yang suku-sukunya positif. Jika U7 – U3 = 24√2 dan U5 = 3√3 U2, suku Ke-6 barisan tersebut adalah …

A. √2
B. √6
C. 3√6
D. 9√2
E. 9√6

Jawaban: E. 9√6
Pembahasan:

Diketahui:

U7 – U3 = 24√2 dan U5 = 3√3 U2

Maka:

U7 = U3 = 24√2
ar6 – ar2 = 24√2
a(r6 – r2) = 24√2 … (i)

U5 = 3√3 U2
ar4 = 3√3 (ar)
r3 = 3√3
r3 = √3

Substitusi r = √3 Ke persamaan (i):

a(r6 – r2) = 24√2
a(27-3) = 24√2
24a = 24√2
a = √2

Karena Itu, suku Ke-6 barisan tersebut adalah:

U6 = ar5 = √2(√3)^5 = 9√6

10. Sebuah bola dijatuhkan Bersama ketinggian 15 m. Setiap kali sesudah jatuh mengenai lantai, bola memantul dan mencapai tinggi 2/3 Bersama tinggi Sebelumnya. Panjang lintasan bola itu sampai berhenti adalah ….

A. 70 m
B. 75 m
C. 80 m
D. 85 m
E. 90 m

Jawaban: B. 75 m
Pembahasan:

Rumus panjang lintasan bola: S∞ = h (q+p/q-p)

S∞ = 15 (3+2/3-2) = 15 (5/1) = 75 m.

11. Nilai x yang memenuhi persaman cos2x – sinx = 0, Sebagai 0° < x < 360° adalah ….

A. {30°, 150°}
B. {30°, 270°}
C. {30°, 150°, 180°}
D. {60°, 120°, 300°}
E. {30°, 150°, 270°}

Jawaban: E. {30°, 150°, 270°}
Pembahasan:

Substitusikan sudut-sudut yang ada Ke pilihan jawaban Ke persamaan.

x = 30° <–> cos 60° – sin 30° = 0 (benar)

Pilihan D salah, kemungkinan A, B, C, dan E benar.

x = 150° <–> cos 300° – sin 150° = cos 60° – sin 30° = 0 (benar)

Tersisa pilihan jawaban A, C, dan E

x = 180° <–> cos 360° – sin 180° = 1-0= 1 (salah)

Tersisa pilihan jawaban tinggal A dan E

x = 270°
<–> cos 540° – sin 270° = cos 180° – sin 270° = -1 – (-1) = 0 (benar)

Maka, jawaban yang benar adalah E.

12. Ke segitiga ABC diketahui 3 sin A + 4 cos B = 6 dan 3 cos A + 4 sin B = 1. Nilai sin C adalah ….

A. 1/2
B. 1/2 √2
C. 1/2 √3
D. √2
E. 1

Jawaban: A. 1/2
Pembahasan:

Identitas Trigonometri: Sin^2α + cos^2 α = 1

Rumus sinus jumlah dan selisih dua sudut sin(α ± β) = sinα x cosβ ± cosα x sinβ

Kuadratkan kedua persamaan yang diketahui:

2 sinA + 4 cosB = 6, jika dikuadratkan:

9 sin^2A + 16 cos^2B + 24 sinA x cosB = 36 …. (i)

3 cosA + 4 sinB = 1, jika dikuadratkan:

9 cos^2A + 16 sin^2B + 24 cosA x sinB = 1 …. (ii)

Jika persaman (i) dan (ii) dijumlahkan, maka:

9 sin^2A + 16 cos^2B + 24 sinA x cosB = 36
9 cos^2A + 16 sin^2B + 24 cosA x sinB = 1
————————————————————– (+)

9 (sin^2A + cos^2A) + 16 (cos^2B + sin^2B) + 24 (sinA x cosB + cosA x sinB) = 37

9(1) + 16(1) + 24 x sin (A+B) = 37
24 x sin(A + B) = 37 -9 – 16
24 x sin (A + B) = 12
sin (A+B) = 1/2

Jumlah sudut Ke segitita = 180°
A + B + C = 180°
C = 180° – (A+B)

sinC = sin (180° – (A+B)) = sin (A+B) = 1/2

13. Suatu prisma persegi Memiliki tinggi 5 dan volume 80.
Berdasarkan informasi Ke atas, pilihlah jawaban Bersama pilihan yang tersedia Ke setiap baris.

1. Luas permukaan prisma sama Bersama 112: Benar / Salah

2. Panjang diagonal ruang prisma lebih Bersama 7: Benar / Salah

3. Suatu bola berdiameter 6 dapat memuat prisma tersebut: Benar / Salah

Jawaban: Benar-Benar-Salah
Pembahasan:

Prisma persegi Memiliki tinggi 5 dan volume 80.

1. Luas permukaan prisma sama Bersama 112

Vprisma = 80 –> La x t = 80 –> s^2×5=80

–> s^2 = 16 –> s = 4

Supaya luas permukaan prisma adalah:

Lprisma = 2s^2 + 4st = 2 x 16 + 4 x 4 x5
Lprisma = 32 + 80 = 112

Pernyataan 1 benar

2. Panjang diagonal ruang prisma lebih Bersama 7.

d = √4^2 + √4^2 + √5^2 = √16 + √16 + √25
d = √57 > √49 = 7

Pernyataan 2 benar

3. Suatu bola berdiameter 6 dapat memuat prisma tersebut.

Sebab panjang diagonal ruang prisma adalah √57, maka bola Bersama diameter 6=√36 tidak dapat memuat prisma tersebut. Panjang diagonal Lprisma > panjang diameter bola. Pernyataan 3 salah.

14. Sebelas siswa mengikuti suatu tes. Guru Mengeluarkan bahwa jangkauan data nilai siswa tersebut adalah 15. Jika diumumkan tiga siswa memperoleh nilai 100, satu siswa memperoleh nilai 96, tiga siswa memperoleh nilai 90, serta dua siswa memperoleh nilai 86, maka nilai dua siswa yang belum diumumkan tersebut paling Mungkin Saja adalah….

A. 99 dan 85
B. 99 dan 88
C. 95 dan 91
D. 89 dan 87
E. 85 dan 84

Jawaban: A. 99 dan 85
Pembahasan:

Diketahui 11 siswa: x1, x2, ….., x11
Jangkauan = x11 – x1 = 15
x11 = x10 = x9 = 100 –> x1 = 85

Jelas, jawaban yang tepat harus memenuhi 85.
Kemungkinan jawaban benar adalah A dan E.
Ingat, x1 adalah nilai terkecil, maka jawaban E salah.

Maka, jawaban yang benar adalah A.

15. Banyak siswa kelas XI A suatu sekolah adalah m. Mereka mengikuti tes Matematika Bersama hasil sebagai berikut. Sepuluh siswa memperoleh skor 100, siswa yang lain memperoleh skor minimal 50, dan rata-rata skor semua siswa adalah 80. Nilai m adalah ….

A. 14
B. 15
C. 16
D. 17
E. 18

Jawaban: C. 16
Pembahasan:

Banyak siswa adalah m
10 siswa Memperoleh nilai 100
Sisanya Menyambut nilai minimal 50, Bersama rata-rata 80, maka dapat dituliskan:

80 = 10(100) + 50(m-10)/m
80m = 1000 + 50m – 500
80m-50m = 1000 – 500
30m = 500
m = 16,66

Karena Itu, nilai m adalah minimal 16.

Itulah 15 contoh soal TKA matematika wajib plus jawaban dan pembahasannya. Selamat belajar!